Complex Impedance
Almost everyone knows about the concept of electrical resistance. Resistance is the ability of a circuit element to resist the flow of electrical current. Ohm’s law defines resistance in terms of the ratio between voltage E and current I.
While this is a well-known relationship, its use is limited to only one circuit element: the ideal resistor. An ideal resistor has several simplifying properties:
- It follows Ohm’s Law at all current and voltage levels.
- Its resistance is independent of frequency.
- AC current and voltage signals though a resistor are in phase with each other.
The real world contains circuit elements that exhibit much more complex behavior. These elements force us to abandon the simple concept of resistance. In its place we use impedance, which is a more general circuit parameter. Like resistance, impedance is a measure of the ability of a circuit to resist the flow of electrical current. Unlike resistance, impedance is not limited by the simplifying properties listed above.
Electrochemical impedance is usually measured by applying an AC potential to an electrochemical cell and measuring the current through the cell. Suppose that we apply a sinusoidal potential excitation. The response to this potential is an AC current signal, containing the excitation frequency and its harmonics. This current signal can be analyzed as a sum of sinusoidal functions (a Fourier series).
Electrochemical Impedance is normally measured using a small excitation signal. This is done so that the cell’s response is pseudo-linear. Linearity is described in more detail in a following section. In a linear (or pseudo-linear) system, the current response to a sinusoidal potential is a sinusoid at the same frequency but shifted in phase.
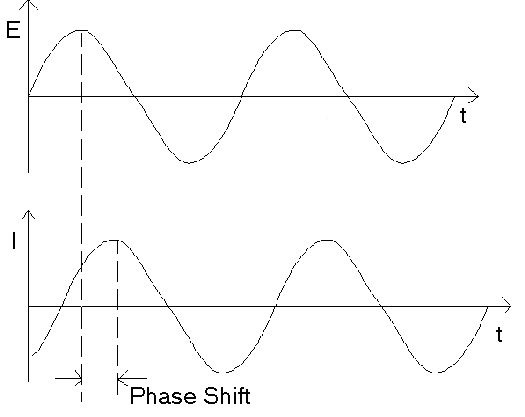
The excitation signal, expressed as a function of time, has the form

E(t) is the potential at time t, E0 is the amplitude of the signal, and ω is the radial frequency. The relationship between radial frequency ω (expressed in radians/second) and frequency f (expressed in hertz) is:
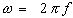
In a linear system, the response signal, It, is shifted in phase (ϕ) and has a different amplitude, I0:
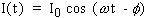
An expression analogous to Ohm’s Law allows us to calculate the impedance of the system as:
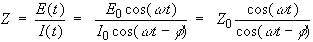
The impedance is therefore expressed in terms of a magnitude, Z0, and a phase shift, ϕ.
If we plot the applied sinusoidal signal on the x-axis of a graph and the sinusoidal response signal I(t) on the y-axis, an oval appears. This oval is known as a Lissajous figure:
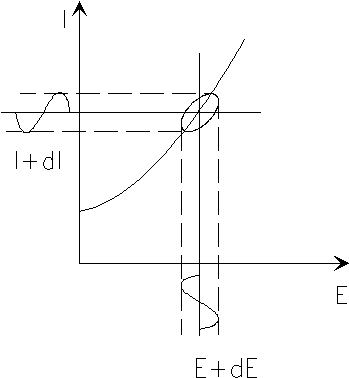
Analysis of Lissajous figures on oscilloscope screens was the accepted method of impedance measurement before the availability of lock-in amplifiers and frequency-response analyzers.
Using Euler’s relationship,
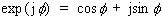
we can express the impedance as a complex function. The potential is described as
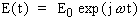
and the current response as
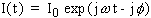
The impedance is then represented as a complex number,
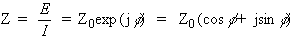

Comments are closed.