Charge-transfer Resistance

A similar resistance to electrolyte resistance is formed by a single kinetically-controlled electrochemical reaction. In this case we do not have a mixed potential, but rather a single reaction at equilibrium.

Consider a metal substrate in contact with an electrolyte. The metal molecules can electrolytically dissolve into the electrolyte, according to:

Me ↔ Men+ + ne–

or more generally:

Red ↔ Ox + ne–

In the forward reaction in the first equation, electrons enter the metal and metal ions diffuse into the electrolyte. Charge is transferred.

This charge-transfer reaction has a certain speed. The speed depends on the kind of reaction, the temperature, the concentration of the reaction products, and the potential.

The general relation between the potential and the current is:

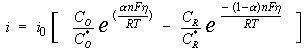
with

i0 = exchange-current density

CO = concentration of oxidant at the electrode surface

CO* = concentration of oxidant in the bulk

CR = concentration of reductant at the electrode surface

F = Faraday’s constant

T = temperature

R = gas constant

α = reaction order

n = number of electrons involved

η = overpotential (E – E0 )

The overpotential, η, measures the degree of polarization. It is the electrode potential minus the equilibrium potential for the reaction.

When the concentration in the bulk is the same as at the electrode surface, CO=CO* and CR=CR*. This simplifies the previous equation into:

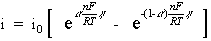
This equation is called the Butler-Volmer equation. It applies when the polarization depends only on the charge-transfer kinetics.

Stirring minimizes diffusion effects and keeps the assumptions of CO=CO* and CR=CR* valid.

When the overpotential, η, is very small and the electrochemical system is at equilibrium, the expression for the charge-transfer resistance changes into:

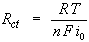
From this equation the exchange-current density can be calculated when Rct is known.