<< Click to Display Table of Contents >> Navigation:  Experiments > G - Electrochemical Impedance > EIS Theory > Equivalent-Circuit Models > Electrical Circuit Elements

Description

EIS data are commonly analyzed by fitting them to a model of an equivalent electrical circuit. Most of the circuit components in the model are common electrical elements such as resistors, capacitors, and inductors. To be useful, the elements in the model should have a basis in the physical electrochemistry of the system. As an example, most models contain a resistor that models the cell's solution resistance.

 

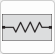
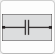
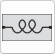
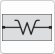
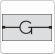
The equivalent-circuit elements that can be used in the Echem Analyst 2™ modeler are shown below. Equations for both the admittance Y and impedance Z are given for each element. The admittance is measured in siemens (S) and is defined as the inverse of the impedance which is measured in ohms (Ω):

 

 

 

•Notice that the impedance of a resistor is independent of frequency and has only a real component. Because there is no imaginary impedance, the current through a resistor is always in phase with the voltage.

•The impedance of an inductor increases as frequency increases. Inductors have only an imaginary impedance component. As a result, an inductor's current is phase shifted 90° with respect to the voltage.

•The impedance versus frequency behavior of a capacitor is opposite to that of an inductor. A capacitor's impedance decreases as the frequency is raised. Capacitors also have only an imaginary impedance component. The current through a capacitor is phase shifted –90° with respect to the voltage.

 

The dependent variables used in these equations are R, C, L, Y0, KA , B, and α. The Electrochemical Impedance Spectroscopy software uses these as fit parameters.

 

Serial and Parallel Combinations

Very few electrochemical cells can be modeled using a single equivalent-circuit element. Instead, EIS models usually consist of a number of elements in a network. Both serial and parallel combinations of elements occur. Fortunately, there are simple formulas that describe the impedance of circuit elements in both parallel and series combinations.

 

Parallel Combinations

For linear impedance elements in parallel you calculate the equivalent impedance from:

 

 

 

Serial Combinations

For linear impedance elements in series, you calculate the equivalent impedance from:

 

 

 

We will calculate two examples to illustrate a point about combining circuit elements. Suppose we have a 1 Ω and a 4 Ω resistor in series. The impedance of a resistor is the same as its resistance as shown in the table above. We thus calculate the total impedance as:

 

 

Resistance and impedance both go up when resistors are combined in series. Now suppose that we connect two 4 μF capacitors in series. The total capacitance of the combined capacitors is 2 μF.

 

 

Impedance goes up, but capacitance goes down when capacitors are connected in series. This is a consequence of the inverse relationship between capacitance and impedance.