A metal covered with an undamaged coating generally has a remarkably high impedance. The equivalent circuit for a scenario like this includes a resistor (primarily caused by the electrolyte) and the coating capacitance in series.

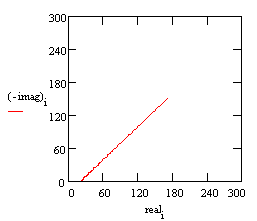
A Nyquist plot for this model is shown below. In making this plot, the following values were assigned:

•R = 500 Ω (a bit high but realistic for a poorly conductive solution)

•C = 200 pF (realistic for a 1 cm² sample, a 25 µm coating, and εr = 6)

•finitial = 0.1 Hz (lowest scan frequency, a bit higher than typical)

•ffinal = 100 kHz (highest scan frequency)

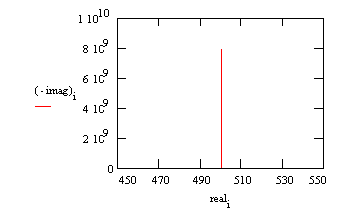Typical Nyquist Plot for an excellent coating.

The value of the capacitance cannot be determined from the Nyquist plot. It can be determined by a curve fit or from an examination of the data points. Notice that the intercept of the curve with the real axis gives an estimate of the solution resistance. The highest impedance on this graph is close to 1010 Ω. This is close to the limit of measurement of most EIS systems. The same data can be shown in a Bode plot.

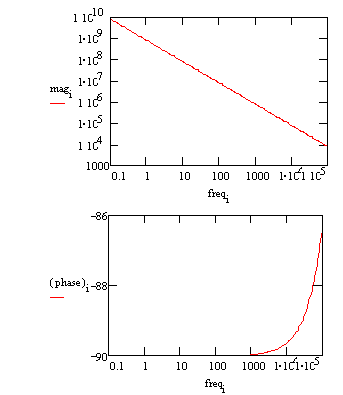Typical Bode Plot for an excellent coating.

The capacitance can be estimated from the graph but the solution resistance value does not appear on the chart. Even at 100 kHz, the impedance of the coating is higher than the solution resistance. Water uptake into the film is usually a fairly slow process. It can be measured by taking EIS spectra at set time intervals. An increase in the film capacitance can be attributed to water uptake.

The Randles cell is one of the simplest and most common cell models. It includes a solution resistance Rs, a double-layer capacitor Cdl and a charge-transfer Rct or polarization resistance Rp. In addition to being a useful model in its own right, the Randles cell model is often the starting point for other, more complex, models.

The following figure is the Nyquist plot for a typical Randles cell. The parameters in this plot were calculated assuming a 1 cm² electrode undergoing uniform corrosion at a rate of 1 mm/year. Reasonable assumptions were made for the β coefficients, metal density and equivalent weight. The polarization resistance under these conditions is calculated to 250 Ω. A capacitance of 40 mF/cm² and a solution resistance of 20 Ω were also assumed.

Nyquist Plot of a Randles circuit modelling a 1 mm/year corrosion rate.

The Nyquist plot for a Randles cell is always a semicircle. You can find the solution resistance by reading the real-axis value at the high-frequency intercept. This is the intercept near the origin of the plot. This plot was generated assuming that Rs = 20 Ω and Rp= 250 Ω. The real-axis value at the other (low-frequency) intercept is the sum of the polarization resistance and the solution resistance. The diameter of the semicircle is therefore equal to the polarization resistance (in this case 250 Ω).

The following figure is the Bode plot for the same cell. The solution resistance and the sum of the solution resistance and the polarization resistance can be read from the magnitude plot. The phase angle does not reach 90° as it would for a pure capacitive impedance. If the values for Rs and Rp were more widely separated, the phase would approach 90°.

Bode Plot of a Randles circuit modelling a 1 mm/year corrosion rate.

First consider a cell where semi-infinite diffusion is the rate-determining step, with a series solution resistance as the only other cell impedance.

A Nyquist plot for this cell is shown below. Rs was assumed to be 20 Ω. The Warburg coefficient calculated to be about 120 Ω/ at room temperature for a two-electron transfer, diffusion of a single species with a bulk concentration of 100 mM, and a typical diffusion coefficient of 1.6 ×10–5 cm²/s. Notice that the Warburg impedance appears as a straight line with a slope of 0.5.

Nyquist Plot of a semi-infinite diffusion process.

The same data can be plotted in the Bode format. The phase angle of a Warburg impedance is 45°.

Bode Plot of a semi-infinite diffusion process.

Adding a double-layer capacitance and a charge-transfer impedance, we get the following equivalent circuit.

This circuit models a cell where polarization comes from a combination of kinetic and diffusion processes. The Nyquist plot for this circuit is shown below. As in the above example, the Warburg coefficient is assumed to be to be about 150 Ω/. Other assumptions: Rs = 20 Ω, Rct = 250 Ω, and Cdl = 40 mF.

Nyquist Plot for a mixed control circuit.

The Bode plot for the same data is also shown below. The lower frequency limit was moved down to 1 mHz to better illustrate the differences in the slope of the magnitude and in the phase between the capacitor and the Warburg impedance. Note that the phase approaches 45° at low frequency.

Bode Plot for a mixed control circuit.

The impedance behavior of a purely capacitive coating was discussed in Model 1: Purely Capacitive Coating. Most coatings degrade with time, resulting in more complex behavior. After a certain amount of time, water penetrates into the coating and forms a new liquid/metal interface under the coating. Corrosion phenomena can occur at this new interface. The impedance of coated metals has been very heavily studied. The interpretation of impedance data from failed coatings can be overly complicated. Only a simple equivalent circuit is discussed here.

Even this simple model has been the cause of some controversy in the literature. Most researchers agree that this model can be used to evaluate the quality of a coating. However, they do not agree on the physical processes that create the equivalent-circuit elements. The discussion below is therefore only one of several interpretations of this model.

The capacitance of the intact coating is represented by Cc. Its value is much smaller than a typical double-layer capacitance. Its units are pF or nF, not mF. Rpo (pore resistance) is the resistance of ion-conducting paths that develop in the coating. These paths may not be physical pores filled with electrolyte.

On the metal side of the pore, we assume that an area of the coating has delaminated and a pocket filled with an electrolyte solution has formed. This electrolyte solution can be quite different from the bulk solution outside of the coating. The interface between this pocket of solution and the bare metal is modeled as a double-layer capacitor Cdl in parallel with a kinetically controlled charge-transfer reaction Rct.

When you use EIS to test a coating, you fit a data curve to this type of model. The fit estimates values for the model's parameters, such as the pore resistance or the double-layer capacitance. You then use these parameters to evaluate the degree to which the coating has failed. In order to show a realistic data curve, we need to do this operation in reverse. Assume that we have a 10 cm² sample of metal coated with a 12 µm film and that we have five delaminated areas. 1% of the total metal area is delaminated. The pores in the film that access these delaminated areas are represented as solution-filled cylinders with a diameter of 30 µm.

The parameters used to develop the curves are shown below:

•Cc = 4 nF (calculated for a 10 cm² area , εr = 6, and thickness = 12 µm)

•Rpo = 3400 Ω (calculated assuming k = 0.01 S/cm)

•Rs = 20 Ω

•Cdl = 4 µF (calculated for 1% of a 10 cm² area and assuming 40 µF/cm²)

•Rct = 2500 Ω (calculated for 1% of a 10 cm² area and using polarization resistance assumptions from an earlier discussion)

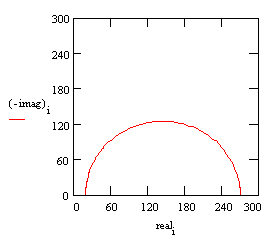
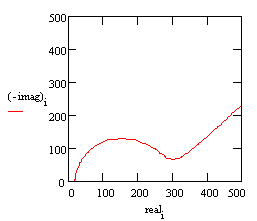
With these parameters, the Nyquist plot for this model shows that there are two well-defined time constants.

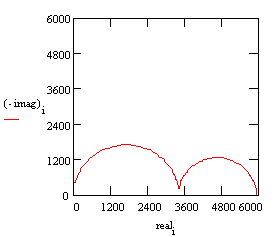Nyquist Plot for a coated metal circuit.

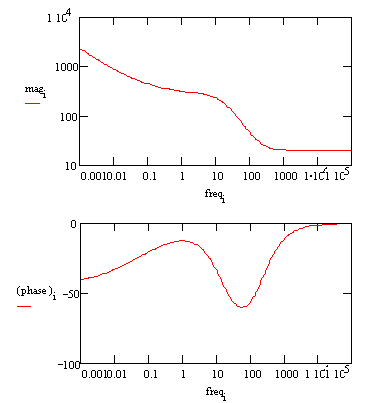
In a Bode plot representing the same data, the two time constants are visible but less pronounced.

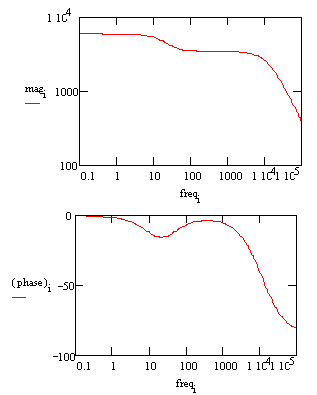Bode Plot for a coated metal circuit.

The Bode plot does not go high enough in frequency to measure the solution resistance. In practice this is not a problem, because the solution resistance is a property of the test solution and the test cell geometry, not a property of the coating. Therefore, it is usually not of interest when testing coatings.